Insurance is a surprising product to me, and it touches a large number of important areas of thought. I want to look closer at insurance, perhaps over the course of multiple blogposts.

The most important and surprising fact about insurance to me is that it is a purely financial arrangement that can create positive value. That’s prima facie kind of surprising, right? Simply by making an agreement that one person will sometimes pay money to another (the insurer to the insured), both parties can end up better off than they were before. Before spending a lot of time thinking about economics, I would not have expected this from transfers: the same money exists no matter who has it. Separate from the surprise, insurance is a good case to look at as a counterexample to bad views that people have about both markets and insurance. Thinking about insurance made me realize that markets are more capable of value creation than I had thought, and that buyers of insurance are on more solid ground than I had thought.

The core idea which has changed my mind, for those who want to skip ahead, is that insurance is a transaction where the insured exchanges expected dollars for expected utility. Insurance can look like an extractive system where insurers charge underinformed policyholders excessive premiums, but in many cases insurance actually is a mutually beneficial reallocation of risk away from policyholders who are less willing to bear it to insurers who are more willing to bear it.

Bad views and intuitions about insurance

I had a bunch of misconceptions about how insurance in particular works, all of which made me think it didn’t make sense to buy. First I thought it was like a lottery ticket. Then I thought it was something that psychologically weak people did because they couldn’t stomach the prospect of loss. It turns out that both of these misconceptions are incomplete and that insurance still makes a lot of sense to buy.

Bad view 1: lottery tickets

I used to think that insurance couldn’t make sense as a product to buy because it was a bet with negative expected value for the buyer, just like a lottery ticket. My reasoning went like this:

Think about lottery tickets. Surely lottery tickets weren’t worth buying, because there are smart people who run the lottery and ensure that the lottery company will make a profit in expectation. And if they’ll make profit in expectation, then buyers of lottery tickets will lose money in expectation. Every lottery ticket has an expected value slightly lower than the price you’d pay for it. The lottery company fiddles with the payout size and odds of winning until they can ensure that every lottery they run will make them money and lose consumers money.

Isn’t insurance just like a lottery ticket? It’s offered by a company run by smart people, a company that assesses risks and charges just enough so that it makes money in expectation, and as a result you the consumer lose money in expectation.

This view turns out to be correct, but, as I’ll explore below, buying insurance still makes sense despite this negative EV (in dollar terms) in most cases.

Bad view 2: psychological security

So if insurance is just a lottery ticket, why would anyone buy it? People would tell me that it provided them a kind of psychological security, and that they slept better at night because they had bought it. This might be true, but I don’t think that insurance is primarily bought as a sleep aid: there are better targeted interventions for those purposes.

I think my view of insurance described below will show that even the least anxious person in the world can benefit from buying insurance. Someone without any inclination toward worry can reduce the likelihood that they'll experience something harmful to them, and realize those benefits in the future rather than in the present.

How insurance actually works

As I said before, the core idea here is that insurance is a transaction where the insured exchanges expected dollars for expected utility. But let’s talk about how that actually works with a couple of examples. I’ll need first to introduce the concept of risk aversion in order to explain how it’s possible for a buyer of insurance to lose out in terms of expected dollars but win in terms of expected utility.

Risk aversion

Risk aversion is a concept whose depth surprised me. I’ll introduce it with an example of playing double or nothing with a coin biased in your favor. If the coin comes up heads (say the coin is biased such that this happens 51% of the time), I give you twice your bet. If the coin comes up tails (49% of the time), I keep your bet. If you bet $1, 51% of the time you win an extra dollar, contributing +$0.51 to your EV, and 49% of the time you lose the dollar you bet, contributing -$0.49 to your EV, so in expectation you win two cents.

Straightforward, right? So now let’s up the bet, since making money only two cents at a time is pretty slow going. If you bet to $10 each time, then you have an expected value of $0.20 by linearity of expectation. If you up the bet to $100 each time, you have an expected value of $2 now, and it’s starting to look like a bet more worth taking. Time is money, though, and all this betting is taking a lot of your time. Maybe you should be more efficient and bet $10,000 at a time so that your expected value is $200 each time.

But what’s that? You don’t want to participate in a $10,000 bet? Even one biased in your favor? Can’t you see that you have an edge and that the math works out in your favor in expectation? What about $100,000? The expected value keeps going up, but it’s seeming like you’re getting more reluctant to participate. What’s going on here? Why are you turning down this chance for free money?

If you were to inspect your feelings about these bets, I’d bet that you’d end up with something like the concept of risk aversion. Losing $10,000 would really suck. It’s a double-digit portion of the American median household income. Losing $100,000 would suck even more: that’s close to the median household wealth in the US.

Risk aversion formalizes the idea that losing a big percentage of your wealth is disproportionately worse than losing a small percentage of your wealth. This is also a corollary to the fact that wealth has diminishing marginal value. That is, the more wealth you have, the less that it will please you to earn an additional dollar. If you have $0 that you can spend, then an additional $100 will improve your life a lot more than it would if you started with $1,000,000.

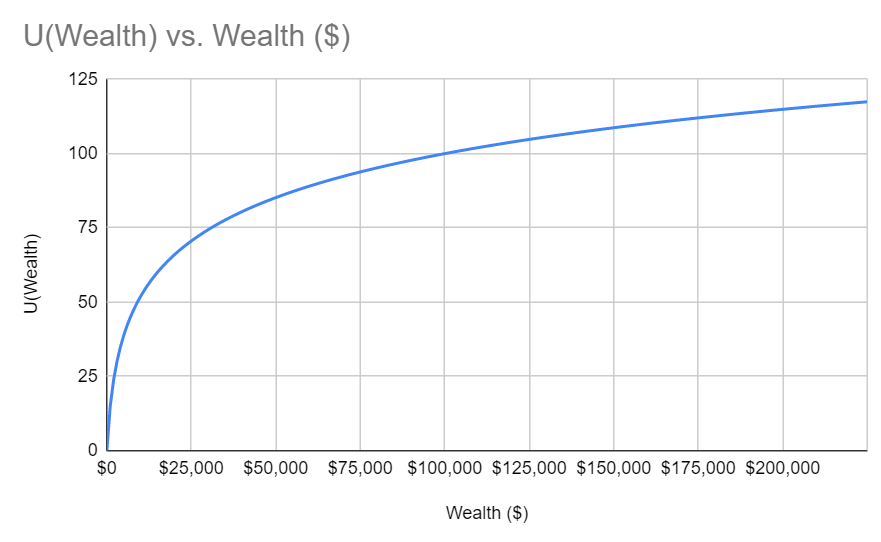
We can draw a curve to represent how much value (we’ll call it utility for now, U) you get out of any amount of money you have (we’ll call that your total wealth, W). To make it clearer that your utility depends on the amount of money you have, we’ll write your utility as a function of your wealth: U(W). The units don’t matter so much, and the shape is maybe off, but this kind of curve is going to drive the rest of the discussion. You can see that the slope decreases as you have more and more money, which reflects that diminishing marginal value of money. The slope of the graph at any value of wealth represents the marginal value of a dollar (how much your utility would go up if you got an additional dollar), and the slope starts very high when you have no wealth and gets shallower as you accumulate more wealth.

So now with this curve we have a visual representation of why you wouldn’t take my $100,000 bet from earlier. If your wealth at the start was $100,000, then losing the bet would make your wealth $0, in which case your utility would be U($0) = 0. Winning the bet would make your wealth $200,000, but because of the diminishing marginal value of wealth, your utility would only be about U($200,000) = 115. So in the case when you win, your utility goes up by 15, and in the case when you lose, your utility goes down by 100, and it turns out that the change in your EV(U(wealth)) as a result of taking the bet is -41.35. That’s not a great bet! If you’re risk averse in the way described by the curve above, you shouldn’t take the bet.

One objection you might have to all of the above is that this risk aversion seems irrational. I don’t exactly know what people mean by “rational” all the time, but it seems very true of myself (and of most people I’ve met) that losing all my wealth would be more than 10x as bad as losing 1/10th of my wealth. If you’re close to retirement and lose 1/10 of your wealth, then you might have to stop eating out at restaurants and miss a vacation or two. If you’re close to retirement and lose all of your wealth, then your life plan is thrown dramatically off course: you might have to move somewhere cheap enough to afford with whatever government benefits you’ll receive, and you’ll likely become extremely dependent on others for the remainder of your life.

One other objection you might have to all the above is that a single utility curve doesn’t make sense and that value is complicated. I’d maybe agree with you, but also you don’t really need to believe that each person has a single utility curve in order to believe that big losses are disproportionately bad.

Now that we understand the basics of risk aversion, we’ll turn to the way it relates to insurance.

The example of insuring your house: exchanging expected dollars for expected utility

Suppose you have a home worth $100k, and that it’s your entire net worth: you don’t have any other assets or debts. Let’s also suppose that you don’t have a great way to earn money to replace it if something bad happens to it. Unfortunately for you, you live in a flood-prone region where over the next year there’s a 5% probability that a flood will destroy your house. An insurance company does the math on insuring your house against flood risk for its entire value, and realizes that there’s a 5% chance they’ll need to pay you $100k and a 95% chance they’ll not need to pay you anything, so the expected cost to them of writing you this insurance policy is 5% * $100k + 95% * $0 = $5k. They have business expenses (computers, offices, salaries) to cover and profits that they want to make, so they’ll probably charge you a little bit more than their strict payout costs, say $1k more, for this insurance policy, bringing the total to $6k.

So how is it that you’re not overpaying for your insurance policy when you agree to pay the $6k? It’s more than the expected value in dollars you’ll get from the policy! This is like a lottery ticket, right?

The answer is no: take a look at the utility curve from above that illustrates risk aversion. Let’s first consider what your expected utility and wealth are like if you don’t buy insurance. If your house floods and you lose it, your only asset, your wealth will be 0 and your utility U(0) will be 0. If your house doesn’t flood, your wealth will remain $100k and your utility will remain U($100k) = 100. Doing the expected value math as in the table below shows that your expected wealth is $95k (0.95 * $100k + 0.05 * $0k = $95k) and your expected utility is similarly 95 (0.95 * 100 + 0.05 * 0 = 95).

If you buy insurance for $6k, though, things are surprisingly different. Whether your house floods or not, you end up with $100k of assets less the $6k you paid for the insurance. If your house doesn’t flood, you still have the $100k house minus $6k you paid for insurance. If your house does flood, you don’t have a house anymore, but your insurance policy pays you out $100k that you can use as you see fit (presumably you’d want to buy another house with it). So no matter what happens, you’ll end up with $100k - $6k = $94k of wealth, and that’s also your EV(W). So you end up with less wealth in expectation if you buy insurance, and it’s by exactly that much that you overpaid for the insurance.

But when we look at the utility curve, we notice that U($94k) is actually pretty high because of the shallow slope of the curve so far away from $0 wealth. We can eyeball the numbers and say that U($94k) = 98. So now when we do the expected utility math, we find that your expected utility in the case where you buy insurance is 98, which is higher than in the case where you didn’t buy insurance!

So, in expectation, by buying insurance, you take your expected wealth EV(W) from $95k to $94k and take your expected utility EV(U(W)) from 95 to 98. You just paid $1k in expectation for 3 utils in expectation. That’s a trade that might be worth taking!

Where does the value come from?

So where do those three utils come from? Does the insurance company make the exact same trade, where it gives up three utils in expectation? The answer is no, but there are two different ways worth framing the answer. The first is to focus on how exactly the insurer ends up losing less utility in expectation than you do, so expected utility is created overall in the system. The second is to focus on how big the gain in expected utility is to you that almost any arrangement that generated that gain for you would have a lower cost overall.

In more detail:

The first frame is that the insurer has a much lower loss of utility when it pays you out, because it has a lot of money to start with. If the insurer is large enough, the $100k payout it would give you if your house floods would be very far out to the right on its utility curve, and so the slope of the utility curve would be very shallow, and so it would have only a very small loss of utility for the $100k payout. If the insurer can ensure enough geographic diversity in the regions where it writes flood insurance policies, then the likelihood that the insurer will have to pay out a painful fraction of its capital will be very low, because a lot of nearly-uncorrelated bets are unlikely to all come out badly at once for the insurer. So it makes sense that for the insurer, the cost in EV(U(W)) terms is negligible.

However, the better frame for this answer is to say that the real value is created in guaranteeing you that you can stay out of the “bad part” of your utility curve. There’s a lot of pain there, and if anyone can guarantee you that you won’t end up there, that’s a huge service to you, and lots of people are clearly willing to pay a lot for that guarantee. If someone can offer that service to you without hurting themselves much, then there’s a lot of value being created. Let’s take a look at the example of mutual insurance to see this a little more clearly.

The example of two-party mutual insurance shows where the value is created

One way to illustrate the value creation going on in insurance schemes is to imagine you and a family member agreeing to insure each other against the flood risk. Let’s suppose you live far apart so that your flood risks are independent of each other. You both have $100k houses, no other assets or liabilities, and identical utility functions that match that graph from earlier. The agreement you make is that you won’t exchange any money upfront, but if someone’s house floods, the other will pay them $50k. That’ll require selling their house and moving to a smaller/worse house.

There are four cases now. If neither of your houses floods, the situation matches the uninsured cases. You each have $100k and 100 utils.

If your house floods and is destroyed, your relative sells his house for $100k, buys himself a new house with $50k, and pays you $50k that you can use to buy a new house. Eyeballing the utility curve, you’ll end up with 85 utils in that scenario (and so will your relative, since he has just as much wealth as you do).

Symmetrically, if your relative’s house floods and yours doesn’t, you do the same: you sell your house for $100k, buy yourself a new house for $50k, and pay the $50k to your relative so that he can buy a new house. Again, you each have $50k and 85 utils.

If both of your houses flood, then nobody has any money and even if you paid each other $50k, the debts would cancel out and you’d still not have any money. You’d each have 0 utils.

The expected value math here is what’s interesting. In short, your expected utility goes up by 3.325 utils by making this arrangement: in the uninsured example above, your expected utility was 95. How does this happen? Well, in only one of the four cases are you worse off than when you didn’t have insurance: when your relative’s house floods and yours doesn’t, and in that case you’re worse off by 15 utils. And this is more than offset by the fact that you’re better off in the opposite case, when your house floods and your relative’s doesn’t flood: in that case you’re better off by 85 utils. Both these cases have the same probability, so the insurance arrangement profits you. And when both of your houses flood, you’re no worse off because of the insurance arrangement: you’d have no money and 0 utils with or without the insurance arrangement.

One other way to summarize what’s going on here with the expected value math is to say that the insurance arrangement has dramatically reduced the likelihood that you will end up in the bad part of the utility function. Without the insurance arrangement, you had a 5% chance of ending up with 0 utility. With the insurance arrangement, you reduce that likelihood to 0.25%. You pay for this by increasing the likelihood that you’ll end up with fewer than 100 utils. Without the insurance arrangement, you had only a 5% chance of ending up with fewer than 100 utils. With the insurance arrangement, you have a 9.75% chance of ending up with fewer than 100 utils, and in the vast majority of those scenarios (9.5% of the 9.75%) you will have 85 utils instead of 100.

So with this example we see that a clever financial arrangement can squeeze out expected utility without any change in expected wealth. This expected utility is created because neither of you wants to be in the bad part of the utility function. You each move probability mass out of the tails of the distribution (where you’d have either 100 utility or 0 utility) and toward the center, where you end up with 85 utility. Because the difference between 0 and 85 is so much greater than the difference between 100 and 85, this works out well in expectation for both of you.

The difference between this arrangement and paying premiums to an insurance company is a little bit complicated: at first blush the insurance company is just a formalized, scaled-up version of this arrangement with some centralized processes and economies of scale. Regardless, there are some advantages to paying premiums to an insurance company: you’ll never lose more money than the premium; by paying premiums in advance you remove a large amount of the counterparty risk (imagine losing your house to a flood, reaching out to your relative, and finding out that he refuses to pay you); and they have prewritten contracts that make it easier to figure out what to do.

The reason that value is created in insurance: what value creation really means and how it relates to GDP calculations

We’ve seen from the above that insurance is a value-creating product. Insurance, even the kind you have to “overpay” for in expected wealth terms, can make you better off in expectation. Your willingness to “overpay” is in some sense a measure of how much value is being created. In the first example, you pay $1k more than you expect to get back from the insurance policy, but you do so willingly because you get in exchange 3 expected utils. Those utils were created from thin air by the financial arrangement you make with the insurance company.

Moreover, you might say that those 3 expected utils have a monetary value to you of exactly the $1k you overpaid by. Suppose also that it costs the insurance company less than $1k in general expenses (over and above expected payout) to provide you the contract (they have to pay for office space, computers, salaries, reinsurance, etc.). This is of course a reasonable assumption: insurance companies tend to be profitable enterprises. If it costs them $800 in general expenses to provide you the contract, then they can book a $200 expected profit, still created largely out of thin air.

Let’s look at that one more time: the insurance company realizes that you have a willingness to pay $6k for a certain contract that will cost them in expectation $5k in expected payouts and $800 of other expenses to administer. There’s $200 of value which didn’t exist before, and that’s just the part booked as a profit on the insurance company’s books. You might have been willing to pay $7k actually for the same policy, but the fact that they charge you only $6k means that you receive the policy which you’d value at $7k for only $6k, a profit of $1k that exists on your books. Each of those expenses paid by the insurance company work the same way: maybe of the $800 of expenses, $400 is the cost of the salesperson who sold you the insurance contract. If the salesperson was actually willing to work for a little less than they were paid (say $380), then the salesperson is also profiting by $20 from the insurance contract.

I worry a bit that I’m venturing into libertarian propaganda now, but in my opinion, the trick that makes all of these transactions into profit generators is the assumption that in general people don’t participate in transactions that make them worse off. The ability to refuse a transaction that you don’t want to participate in makes it the case that you’ll only engage in it if it will make you better off. The amount by which you’re better off varies, but it’ll always be at least 0.

Everywhere you look at (freely entered) transactions, there are these little premiums being charged and captured as people end up more willing to provide goods and services to others than keep them for themselves. These are gains from trade and comparative advantages. This is what it looks like for wealth to be created. It’s not the mere dollars flowing through the economy that matters, it’s the premiums charged at every step of the way as preferences are met and willingness to pay exceeds cost to provide.

There are important caveats. Exploitation is possible and bad. Not every transaction is freely entered, and people make mistakes sometimes which cause them to lose money. Forecasting is hard. Regardless, this is an important framework for understanding how value is created in transactions.

Useful takeaway: a guide for buying insurance

On my view of insurance, you should buy insurance only if at least one of the following is true:

1. If the loss you’re buying insurance against is actually catastrophic and you'd willingly overpay in expected dollars to underpay in expected utility. This is the example we discuss above. Many classic kinds of insurance fit into this bucket, including some forms of health insurance.

2. If you can adversely select yourself into the insurance pool: you think you're substantially more likely than average to require a payout. If this is the case, then you’re no longer predicting that your purchase of the insurance is a win-win; you think you’re going to win at the insurer’s expense in expectation.

If you’re being offered insurance for some plane tickets you’re buying, the insurer is unlikely to offer it at an expected financial loss to themselves. So you can be reasonably sure that it’s priced such that it will make money for the insurer on average. All the insurance will do for you is reimburse you for various expenses, and those expenses are unlikely to be catastrophically large for you. Only if you think you’re unusually likely to miss your flight and gain the payout would it make sense for you to buy the insurance, in my opinion.

3. If the insurance will save you a big administrative burden in the payout scenario. A lot of times, insurers will handle legal claims or find people to repair your stuff. That logistical coordination is hard and difficult, and lots of people would rather pay money (in the form of insurance that costs more than dollars it will pay out in expectation) than do the coordination themselves.

4. If it's legally required. Many such cases!

5. If you get a big subsidy.

There are a lot of insurance-like products out there that more like a pre-payment plan for costs that are pretty likely to be incurred (e.g. vision or dental insurance). People often say things like "auto insurance doesn't pay for your gas" to point to the distinction between the kind of insurance that pays out for rare events and the kind that doesn't. Many kinds of insurance are in that second bucket, and are just a fancy form of pre-payment. A lot of the time, a pre-payment plan doesn't make much sense unless there's some reason they'll administer it more cheaply than you'd be able to administer it yourself. But in a lot of cases, these plans get tax benefits under U.S. law, and employers are often incentivized by law to subsidize them. In those cases, it makes a lot of sense to buy the plans.

Conclusion

That's the post! I will likely continue writing more about insurance in the coming weeks.